Particle-size distribution model wherein random samples are drawn from the doubly-truncated univariate normal probability density function: More...

Inheritance diagram for normal:

[legend]

Collaboration diagram for normal:

[legend]

Public Member Functions
	TypeName ("normal")

	normal (const dictionary &dict, Random &rndGen)

	normal (const normal &p)

virtual autoPtr< distributionModel >	clone () const

void	operator= (const normal &)=delete

virtual	~normal ()=default

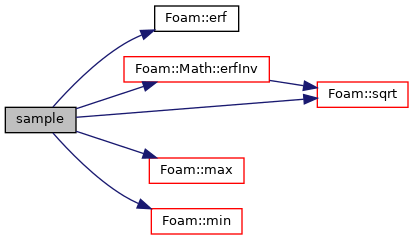
virtual scalar	sample () const

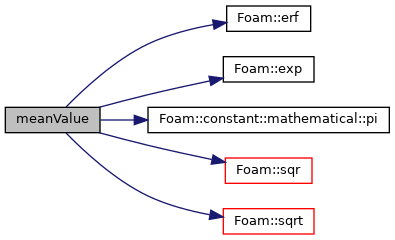
virtual scalar	meanValue () const

Public Member Functions inherited from distributionModel
	TypeName ("distributionModel")

	declareRunTimeSelectionTable (autoPtr, distributionModel, dictionary,(const dictionary &dict, Random &rndGen),(dict, rndGen))

	distributionModel (const word &name, const dictionary &dict, Random &rndGen)

	distributionModel (const distributionModel &p)

virtual	~distributionModel ()=default

virtual scalar	minValue () const

virtual scalar	maxValue () const

Additional Inherited Members
Static Public Member Functions inherited from distributionModel
static autoPtr< distributionModel >	New (const dictionary &dict, Random &rndGen)

Protected Member Functions inherited from distributionModel
virtual void	check () const

Protected Attributes inherited from distributionModel
const dictionary	distributionModelDict_

Random &	rndGen_

scalar	minValue_

scalar	maxValue_

Detailed Description

Particle-size distribution model wherein random samples are drawn from the doubly-truncated univariate normal probability density function:

$f(x; \mu, \sigma, A, B) = \frac{1}{\sigma} \frac{ \phi \left( \frac{x - \mu}{\sigma} \right) }{ \Phi \left( \frac{B - \mu}{\sigma} \right) - \Phi \left( \frac{A - \mu}{\sigma} \right) }$

where

$f(x; \mu, \sigma, A, B)$	=	Doubly-truncated univariate normal distribution
$\mu$	=	Mean of the parent general normal distribution
$\sigma$	=	Standard deviation of the parent general normal distribution
$\phi(\cdot)$	=	General normal probability density function
$\Phi(\cdot)$	=	General normal cumulative distribution function
	=	Sample
	=	Minimum of the distribution
	=	Maximum of the distribution

Constraints:

$\infty > B > A > 0$
$x \in [B,A]$
$\sigma^2 > 0$

Random samples are generated by the inverse transform sampling technique by using the quantile function of the doubly-truncated univariate normal probability density function:

$x = \mu + \sigma \sqrt{2} \, {erf}^{-1} \left( 2 p - 1 \right)$

with

$p = u \, \left( \Phi\left( \frac{B - \mu}{\sigma} \right) - \Phi\left( \frac{A - \mu}{\sigma} \right) \right) + \Phi\left( \frac{A - \mu}{\sigma} \right)$

$\Phi(\xi) = \frac{1}{2} \left( 1 + {erf}\left(\frac{\xi - \mu}{\sigma \sqrt{2} }\right) \right)$

where $ u $ is sample drawn from the uniform probability density function on the unit interval $ (0, 1) $ .

Reference:

        Governing expressions (tag:B):
            Burkardt, J. (2014).
            The truncated normal distribution.
            Department of Scientific Computing Website,
            Florida State University, 1-35.
            URL:people.sc.fsu.edu/~jburkardt/presentations/truncated_normal.pdf
            (Retrieved on: 19 Feb 2021)

Usage

Minimal example by using constant/<CloudProperties>:

subModels
{
    injectionModels
    {
        <name>
        {
            ...

            sizeDistribution
            {
                type        normal;
                normalDistribution
                {
                    mu        <mean>;
                    sigma     <stardard deviation>;
                    minValue  <min>;
                    maxValue  <max>;
                }
            }
        }
    }
}

where the entries mean:

Property	Description	Type	Reqd	Deflt
`type`	Type name: normal	word	yes	-
`normalDistribution`	Distribution settings	dict	yes	-
`mu`	Mean of the parent general normal distribution	scalar	yes	-
`sigma`	Standard deviation of the parent general normal distribution	scalar	yes	-
`minValue`	Minimum of the distribution	scalar	yes	-
`maxValue`	Maximum of the distribution	scalar	yes	-

Note

The mean and standard deviation of the parent general normal probability distribution function (i.e. input) are not the same with those of the truncated probability distribution function.

Source files

Definition at line 244 of file normal.H.